The God Protocols
Imagine the ideal protocol. It would have the most trustworthy third party imaginable – a diety who is on everybody’s side. All the parties would send their inputs to God. God would reliably determine the results and return the outputs. God being the ultimate in confessional discretion, no party would learn anything more about the other parties’ inputs than they could learn from their own inputs and the output.
Alas, in the our temporal world we deal with humans rather than deities. Yet, too often we are forced to treat people in a nearly theological manner, because our infrastructure lacks the security needed to protect ourselves.
Trusted Third Party
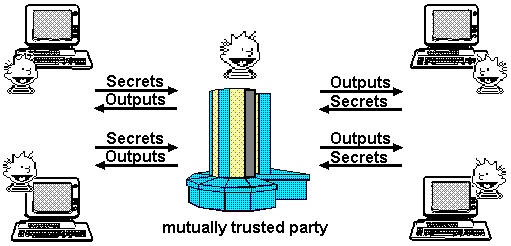
Network security theorists have recently solved this problem to an astonishing extent. They have developed protocols which create virtual machines between two or more parties. Multiparty secure computation allows any number of parties to share a computation, each learning only what can be inferred from their own inputs and the output of the computation. These virtual machines have the exciting property that each party’s input is strongly confidential from the other parties. The program and the output are shared by the parties.
For example, we could run a spreadsheet across the Internet on this virtual computer. We would agree on a set of formulas and set up the virtual computer with these formulas. Each participant would have their own input cells, which remain blank on the other participants’ computers. The participants share output cell(s). Each input our own private data into our input cells. Alice could only learn only as much about the other participants’ input cells as she could infer from her own inputs and the output cells.
Mathematically Trustworthy Protocol
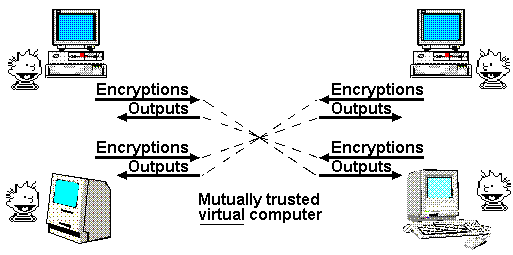
There are three major limitations. The first is that this virtual computer is very slow: in some cases, one arithmetic calculation per network message. Currently it is at best practical only for small logic or arithmetic calculations used as an adjunct to or component of more efficient computations and protocols.
The second is that there is a tradeoff between privacy, fairness, and fault tolerance. Fairness means everybody learning the results in such a way that nobody can gain an advantage by learning first. Fault tolerance can provide robustness against a minority, so that it takes a majority dropping out to halt the protocol, or it can be nonrobust but fail-stop, so that a single participant can terminate the protocol. Many papers have discussed the fraction of parties one must trust in order to be assured of learning the correct output. In traditional results, fairness and privacy could not both be achieved with a faulty majority. Recent papers[3][4][5][6] have produced fair and private protocols even with faulty majorities. They trade robustness for privacy and fairness against any proportion of faulty parties. The advantage of this fail-stop approach is that one can usually find new partners and start over again, but one does not want to suffer irreversible losses such as leaking information, being left holding the bag, or being convinced of an incorrect result.
The third limitation is that, far from being omniscient or omnipotent, the protocol will accomplish only what is specified in the algorithm and the inputs. It won’t be able to replace human trusted third parties where those parties provide insight or knowledge that cannot be provided by a computer.
With these caveats, any algorithmic intermediary can, in principle, be replaced by a trustworthy virtual computer. In practice, because of the three complications, we usually construct more limited protocols out of more efficient elements.
Multiparty computation theory, by making possible privy virtual intermediation, has major implications, in theory, for all kinds of contractual relationships. This can be seen most clearly in the area of negotiations. A “mechanism” in economics is an abstract model of an institution which communicates with its participants via messages, and whose rules can be specified algorithmically. These institutions can be auctions, exchanges, voting, and so on. They typically implement some kind of negotiation or decision making process.
Economists assume a trusted intermediary operates the mechanism. Here’s a simple example of using this virtual computer for a mechanism. Alice can submit a bid price, and Bob an ask price, then their shared virtual program which has one instruction, “A greater than B?”. The computer then returns “true” if Alice’s bid is greater than Bob’s offer. A slightly more sophisticated computer may then decide the settlement price according to a number of different algorithms (Alice’s bid, Bob’s ask, split the difference, etc.) This implements the mechanism “blind bargaining” with no trusted intermediary.
In principle, since any computable problem can be solved on this virtual computer (they are “Turing complete”), any computable economic mechanism can be implemented without a trusted intermediary. In practice, we face the three limitations discussed above. But the existence proof, that any economic mechanism can be run without a trusted intermediary, is very exciting. This means that, in principle, any contract which can be negotiated through a trusted third party (such as an auction or exchange) can be negotiated directly. So, in some abstract sense, the only remaining “hard” problems in smart contract negotiations are (a) problems considered hard even with a trusted intermediary (for the standard economic reasons), and (b) the task of algorithmically specifying the negotiating rules and output contract terms (This includes cases where an intermediary adds knowledge unavailable to the participants, such as a lawyer giving advice on how to draft a contract). In practice, many problems which can be solved in principle with multiparty computation will re-arise when we implement protocols in an efficient, practical manner. The God Protocols give us a target to shoot for.
Applying this kind of analysis to the performance phase of contracts is less straightforward. For starters, economic theories of the performance phase are not as well developed or simple as the mechanism theory of negotiations. Indeed, most economic theory simply assumes that all contraccts can be perfectly and costlessly enforced. Some of the “transaction cost” literature has started to move beyond this assumption, but there are few compelling results or consensus theories in the area of techniques and costs of contract enforcement.
Performance phase analysis with multiparty secure computer theory would seem to apply only to those contracts which can be performed inside the virtual computer. But the use of post-unforgeable auditing logs, combined with running auditing protocols inside the shared virtual computer, allows a wide variety of performances outside the virtual computer to at least be observed and verified by selected arbitrators, albeit not proactively self-enforced.
The participants in this mutually confidential auditing protocol can verify that the books match the details of transactions stored in a previously committed transaction log, and that the numbers add up correctly. The participants can compute summary statistics on their confidentially shared transaction logs, including cross-checking of the logs against counterparties to a transaction, without revealing those logs. They only learn what can be inferred from the statistics, can’t see the details of the transactions. Another intriguing possibility is that the virtual computer can keep state over long periods of time, allowing sophisticated forms of privy and self-enforcing secured credit.
If mutually confidential auditing ever becomes practical, we will be able to gain high confidence in the factuality of counterparties’ claims and reports without revealing identifying and other detailed information from the transactions underlying those reports. These would provide the basis for solid reputation systems, and other trusted third party systems, that maintain integrity across time, communications, summarization, and preserve confidentiality for transaction participants. Knowing that mutually confidential auditing can be accomplished in principle will hopefully lead us to practical solutions to these important problems.
References
-
D. Chaum, C. Crépeau, and I. Damgaard, Multiparty unconditionally secure protocols; In 19th Symp. on Theory of Computing, pages 11-19. ACM, 1988.
-
"The Spymasters Double Agent Problem: Multiparty Computations Secure Unconditionally from Minorities and Cryptographically from Majorities," D. Chaum, Advances in Cryptology CRYPTO'89, G. Brassard (Ed.), Springer-Verlag, pp. 591-601.
-
C. Crépeau, J. van de Graaf, and A. Tapp, Committed Oblivious Transfer and Private Multi-Party Computations; Advances in Cryptology: Proceedings of Crypto '95, Springer-Verlag, pages 110-123, 1995. ↩
-
Complete Characterization of Adversaries Tolerable in Secure Multi-Party Computation, Martin Hirt and Ueli Maurer. Computer Science Department, ETH Zürich. 1997. in Proceedings of PODC '97 ↩
-
Matthias Fitzi, Martin Hirt, and Ueli Maurer: Trading correctness for privacy in unconditional multi-party computation. In Advances in Cryptology — CRYPTO '98, volume 1462 of Lecture Notes in Computer Science, 1998. ↩
-
R. Cramer, I. Damgaard, S. Dziembowski, M. Hirt, T. Rabin, Efficient Multi-Party Computations with Dishonest Majority, Proceedings of Eurocrypt '99, Springer Verlag LNCS, to appear (May '99). ↩
Please send your comments to nszabo (at) law (dot) gwu (dot) edu
Copyright © 1997-1999 by Nick Szabo
Permission to redistribute without alteration hereby granted