Public-Key Cryptography

Chapter 1: The Strategy

Symmetric-Key Cryptography

Public-key cryptography is the greatest tool of liberty ever devised. Its discovery was revolutionary. Before then, all cryptography was just hacks. It was developed in 1973 by Ellis, Cocks, and Williamson at researchers at CGHQ in the UK, but this work was classified until 1997. It was developed independently 1976 by Rivest, Shamir, and Adleman at MIT. Their work was published, although it was protected by a patent until 2000. Finally it is free.

To understand it, however, it will be necessary to go over the basics of symmetric-key cryptography, which is the sort of cryptography we are intuitively familiar with, the kind that has existed since antiquity. Once the limitations of symmetric-key cryptography are understood, then public-key cryptography will seem like magic.^[1]

Begin by thinking about the idea of a simple substitution cypher. This means that the message is a string of text and encryption consists of replacing each letter with a different one. For example, can you solve the following code?

JHBYEUXRBLPDWJXOBELNEHNTBFYDJHBWDCYUWJWLNUUWZBDJXLYERWRJRWEIBBCWEGJHBWDOYEBXWEJHBWDYSECYLIBJRUXRNEMBDRCYYEBD

Two things to note here. First, this algorithm is insecure. Regardless of how the letters are replaced, it would be easy to decipher, especially with a computer. We will need something much more complicated to make a message that is secret enough. More importantly, however, is that knowing the sequence of letter replacements is sufficient both to decrypt and to encrypt a message. It is, in fact, impossible to know how to encrypt a message without simultaneously knowing how to decrypt it.

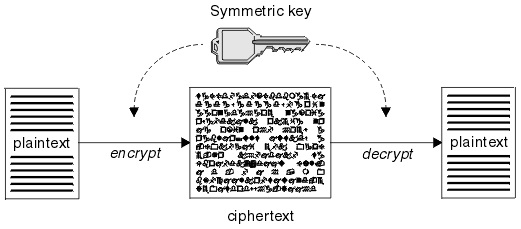
This is the essence of symmetric-key cryptography: it is impossible to know how to encrypt a message without knowing how to decrypt it, and vice versa. This is a real problem. If, for example, my enemy got ahold of one of my secret messages and managed to decipher it, he would not only be able to read the rest of my messages but make new ones, perhaps to trick me and my friends.

However, more fundamentally it is a problem because if the only encryption we know is symmetric-key encryption, then there is no way to relay message at all. Two confederates have no way of talking to one another to establish a secret protocol which would not give up everything to an interloper. We must already possess a secure means of communication in order to securely discuss a symmetric-key code! But if we had that, then the problem would already be solved.

Symmetric-key cryptography is thus really useful only for keeping secrets to yourself and away from all others. The moment you let someone else in on it, you have created a security hole. You do not know who might be listening, and you do not know who else may get the secret from your confederate.

Asymmetric-Key Cryptography

Let us think about how to improve upon the substitution cypher. One of the most obvious tricks we might try is to replace letters in blocks of two rather than individually. For example, AA might become QF and BB might become LV. This would be much more secure although still easily broken with the help of a computer. We might then try replacing letters in blocks of three or four. Eventually we would reach a point that would be impossible for even a computer to break in a reasonable time.

However, the problem with this method is that the larger the block we use, the larger is the list of substitutions. A block of two requires 26^2==676 replacements. A block of three would take 17,576 replacements, and block of four would take almost half a million. A computer could not break such a code, but to communicate such an enormous list would not be at all practical to do securely.

Instead, we might try to concoct an algorithm that jumbles up a block of four letters in some way that would be very difficult to guess but which can be described in a very short message. This really opens up new possibilities: because a substitution cypher is given simply as a list of replacements, it is inherently a symmetric key algorithm. Whereas, if a cypher is given as an algorithm, and if the set of replacements it defines is so enormous that it could not practically be enumerated, then the properties of the algorithm can utterly change the properties of the cypher.

For example, suppose you could design an algorithm that can run in a fraction of a second but whose inverse algorithm would takes millions of years. If you had something like that, you could safely explain it to anyone and without fear that the message would be decrypted. Not terribly useful because no one, even me or my friends, can decrypt any messages at all! Still interesting, though.

However, there is an upgrade to this idea that makes it useful. Suppose there are two algorithms which are inverses of one another. Both are fast to do forward and very slow to reverse. One algorithm can be used to encrypt and the other to decrypt. I keep the decryption algorithm secret but let my friends see the encryption algorithm. Now they can send me messages but only I can read them, and I have not given away any secrets that I cannot afford to have compromised. In fact, I can let my enemies see the encryption algorithm too. They can do nothing with it but make their own messages to me.

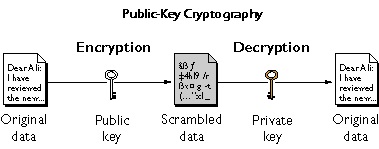
The final upgrade is that everyone has two algorithms. Everyone keeps one algorithm secret and publicizes the other. How can we discover so many algorithms? Typically there is a class of algorithms, each of which is specified by a number, or key. So we each have a public key and a private key. This is public-key encryption.

Now any two people can communicate securely even if they do not begin with a secure channel. An enemy may have his ear right in our faces, but he can understand nothing of what we say to one another after we have exchanged public keys.

Building Communities With Public Key Cryptography

The magic of public-key cryptography comes from the fact that it gives people the ability to prove that they have a secret without revealing it. Think about how paradoxical that sounds for a moment. Yet it is quite easy to understand now. If I wish to verify your identity, I simply send you a message encrypted by your public key and ask you to tell me what the message said. Only the holder of the private key can answer the question correctly.

This seems nonintuitive to us because our technology does not rely on it. The fact that we still use such primitive technologies today like credit cards, which have their number printed right on them, or forms of identification such as social security numbers is backwards. They have been obsolete for decades. There should never be a reason to show your password or identity number to anyone else, ever.

The reason public-key cryptography is so empowering to the individual is that you prove your identity only with your consent. A private key is not like an ID card that can be demanded at any time and forced out of you if necessary. You choose which groups you wish to belong to and you can keep your membership secret.

There is a slight problem here. If there is a third party listening when you exchange public keys, he sees which public keys are exchanged. Even if he does not see you prove your identity, won’t that be enough for him to assume that the public keys correspond to the private keys? This is easily resolved because the key that you use for authentication does not have to be the same as the one used to establish a secure channel. You can even generate a new key randomly with each conversation and then authenticate yourself with your permanent private key.^[2]

There’s more. If you use your private algorithm on a message encrypted with your public algorithm, you get the original message back. Since the two algorithms are inverses of one another, you could also use your private algorithm on a unencrypted message to get an encrypted message that can only be decrypted by your public algorithm. The result is an encrypted message that is veritably mine. This is the idea behind a digital signature.

The use of a digital signature is that the community can require them for certain kinds of communications, for whatever it considers important for establishing the reputation of its members. Messages can be digitally signed by several people, so they can be treated as contracts or records of a trade. Each member’s history can be public and unforgettable.

A real digital signature is slightly more complicated than what I have described here. Normally one would not encrypt an entire message but instead a short of the message. The message is sent with its encrypted hash. The effect is the same because the message is still indelibly tied to the sender.

A community which combines cryptographic secrecy, public-key authentication, and digital signatures is a voluntary community tied together by contracts and reputation. It requires no central authority because the records it relies on to establish reputation can be stored on many different computers. Thus, it is resilient against government attack. Banishment is the only punishment the community has available.

This is libertarianism. It is exactly what libertarians have always yearned for. If we want people to get used to the idea that they can brush government aside and that freedom of association and privacy are inherent in the nature of reality, all we must do is build cryptographic communities. There is no need to speak in abstract terms with people who won’t listen until we turn blue. Just build the networks and people will be attracted to them. Once people get used to them, they will demand them.

There is one other service people might want that I have not provided for: anonymity. An interloper may not know what you are saying, but he might still know that you are a member. Maybe a spy can become a member himself and try to tie a real-life person to a public key. Ideally, you might want to prevent your communications from being linked to the community at all. Anonymity is a little bit trickier to provide, but it can be achieved with services like Tor. I do not wish to go into more detail about what is possible, but suffice to say there is much more that can be built upon the basic structure I have described here.

Chapter 3: The Killer App of Liberty

Chapter 4: The Risk From the Software Industry